Все воздухоплавание основано на законе Архимеда. На любой предмет, находящийся в атмосфере, действует подъемная сила, равная весу воздуха, вытесненного этим предметом. Полная подъемная, или Архимедова, сила теплового аэростата равна:
Fa=(Mн-Мв)g (1)
где Мн - масса воздуха окружающей среды, вытесненная оболочкой аэростата; Мв - масса теплого воздуха, находящегося в оболочке; g - ускорение силы тяжести. g=9,8 м/с2.
Массы Мн и Мв можно выразить через плотность воздуха и объем оболочки:
Мн=ρнV
(2)
Мв=ρвV
(3)
где V - объем оболочки; ρн и ρв - соответственно плотность воздуха окружающей среды и плотность воздуха внутри оболочки.
Из уравнения Менделеева—Клапейрона можно получить связь между плотностью, давлением и температурой:
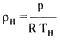 (4)
(4)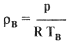 (5)
(5)
где р - давление окружающей среды; Тн и Тв - соответственно температура наружного, или окружающею, воздуха и температура внутри оболочки в градусах Кельвина; R - газовая постоянная воздуха, для сухого воздуха R=287 Дж/кг·град.
Окончательно полную подъемную силу аэростата (1) с учетом (2)...(5) можно записать в следующем виде:
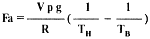 (6)
(6)
Из формулы (6) видно, что с уменьшением давления подъемная сила аэростата уменьшается, а при уменьшении температуры наружного воздуха она возрастает.
Необходимо обратить внимание на то, что все используемые переменные должны быть выражены в Международной системе SI, при этом подъемная сила Fa будет измеряться в ньютонах.
Для тех величин, которые были использованы выше, в системе SI применяются следующие единицы измерения:
- для массы - кг (М = [кг]);
- для температуры - градус Кельвина (Т = [К];
- для силы и веса - ньютон (F = [Н] = [кг м/с2];
- для плотности - кг/м3 (г = [кг/м3]);
- для объема - м3 (V = [м3]);
- для давления - паскаль (р = [Па] = [Н/м3]).
Чтобы перевести привычные слинтшы измерения в единицы измерения системы SI, можно воспользоваться следующими простыми выражениями:
Т[К] = 273 + t[C];
рПа] = 133,3 р[мм рт. ст];
р[Па] = 9,8
р[мм вод. ст);
F[кг] = F[H]/9,8.
В квадратных скобках указаны соответствующие единицы измерения, так, если температура в градусах Цельсия равна 15 град., то в градусах Кельвина она будет 273+15=288, давление 760 мм рт. ст. будет соответствовать 101 300 Па.
Иногда, например с целью сравнения с предельно допустимой, требуется определить температуру в оболочке аэростата. В этом случае из выражения (6) не сложно получить соответвующее значение:
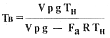 (7)
(7)
Приведенными формулами можно пользоваться для различных условий полета, необходимо лишь знать зависимость между высотой, давлением и температурой и помнить, что все величины в выражениях необходимо подставлять в системе SI. В Каждом конкретном случае в реальных условиях могут реализовываться различные соответствия между этими параметрами атмосферы, однако в среднем существует общая закономерность, связывающая высоту, давление и температуру, которая определяется Международной стандартной атмосферой (МСА). Небольшая выдержка из МСА приведена в таблице 5.1.
Таблица 5.1 Международная стандартная атмосфера
|
Высота, |
Давление, |
Температура, | ||
|
0 |
760 |
101300 |
15,0 |
288 |
|
1000 |
674 |
89870 |
8,5 |
281,5 |
|
2000 |
596 |
79490 |
2,0 |
275 |
|
3000 |
526 |
70100 |
-4,5 |
268,5 |
|
4000 |
462 |
61630 |
-11 |
262 |
|
5000 |
405 |
54010 |
-17,5 |
255,5 |
|
6000 |
354 |
47170 |
-24 |
249 |
|
7000 |
308 |
41050 |
-30,5 |
242,5 |
Из простых примеров 5.1...5.3. следует, что при изменении температуры наружного воздуха на 10 градусов подъемная сила аэростатов с объемом оболочки 2180м3 (класс АХ-7) изменяется на 703-607=96 кг, т.е. почти на сто килограмм, а при изменении на эту же величину температуры внутри оболочки подъемная сила изменяется лишь на 607-551=56 кг. Следовательно, при тех условиях, в которых наиболее часто эксплуатируется аэростат, влияние температуры наружного воздуха на подъемную силу почти в два раза больше, чем влияние температуры в оболочке.
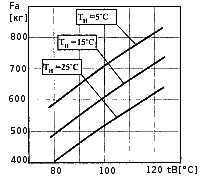 |
Наиболее наглядно зависимость полной подъемной силы аэростата класса АХ-7 от температуры наружного воздуха и температуры в оболочке показана на рис. 5.1. Рис. 5.1. Зависимость подъемной силы аэростата от температуры наружного воздуха tн и температуры в оболочке tв для объема V=2180м3 |
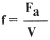
Из уравнений (1)...(5) следует:
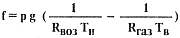
где Rвоз и Rгаз - соответственно газовые постоянные воздуха и газa в оболочке [Дж/кг·град]; f - удельная подъемная сила в Н/м3.
Для любого газа его газовая постоянная равна отношению универсальной газовой постоянной (8314 Дж/кг·град) к молекулярному весу.
Значения газовых постоянных приведены в таблице 5.2.
Проведенные по формуле (8) расчеты приведены в таблице 5.3.
Таблица 5.2 Газовые постоянные, Дж/кг·град
|
Воздух |
Вода |
Метан |
Гелий |
Водород |
|
287 |
462 |
520 |
2079 |
4158 |
Таблица 5.3 Значения удельной подъемной силы им различных газов при температуре наружного воздуха 15°С и высоте над уровнем моря Н=0 м
|
Темпе- |
Удельная подъемная сила, кг/м3 | ||||
|
воздух |
вода |
метан |
гелий |
водород | |
|
20 |
0.021 |
— |
0.559 |
1.057 |
1.140 |
|
40 |
0.098 |
— |
0.602 |
1.068 |
1.145 |
|
60 |
0.165 |
— |
0.639 |
1.077 |
1.150 |
|
80 |
0.225 |
— |
0.672 |
1.085 |
1.154 |
|
100 |
0.279 |
0.636 |
0.702 |
1.093 |
1.158 |
|
120 |
0.327 |
0.666 |
0.728 |
1.099 |
1.161 |
|
140 |
0.370 |
0.693 |
0.752 |
1.105 |
1.164 |
|
160 |
0.410 |
0.718 |
0.774 |
1.111 |
1.167 |
|
180 |
0.445 |
0.740 |
0.794 |
1.116 |
1.169 |
|
200 |
0.478 |
0.760 |
0.812 |
1.120 |
1.172 |
Если внимательно посмотреть на таблицу 5.3, то можно увидеть,
что:
- в диапазоне температур от 80 до 120 градусов удельная подъемная сила воздуха составляет 20...30% от подъемной силы самого легкого газа - водорода;
- подъемная сила воздуха с ростом температуры изменяется более интенсивно, чем других газов;
- пары воды обладают значительной подъемной силой, что может быть использовано в перспективных разработках тепловых аэростатов, когда в оболочку через специальные форсунки впрыскивается вода.
На практике всегда бывает известна стартовая масса аэростата и объем его оболочки. Подъемная сила одного кубометра в этом случае является постоянной величиной, не зависящей от высоты полета (если пренебречь расходом топлива), поэтому для пилота важно знать, как будет изменяться потребная температура внутри оболочки при изменении высогы полета.
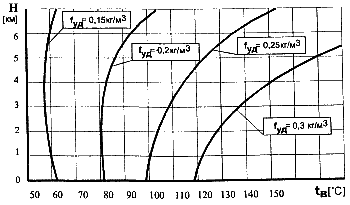 |
Для условий стандартной атмосферы эта зависимость показана на рисунке 5.2, из которой следует, что при различных загрузках аэростата (различных удельных подъемных силах) потребная температура в оболочке имеет различный вид. При ни рузках более 0,25 кг/м3 потребная температура в оболочке начинает расти сразу по мере увеличения высоты полета, при малых загрузках (менее 0,2) температура в оболочке до некоторых высот уменьшается. Рис. 5.2. Зависимость температуры в оболочке tв от высоты полета Н и удельной подъемной силы ƒуд для стандартной атмосферы |
Величина удельной подъемной силы 0,25 кг/м3, как правило, используется при первых, оценочных, расчетах объемов оболочек тепловых аэростатов.
Выше было подробно рассмотрено влияние всех основных факторов на подъемную силу, в то же время иногда возникает вопрос о влиянии влажности. Чисто качественно ответ на этот вопрос достаточно простой, так как влажный воздух легче сухого, то с увеличением влажности подъемная сила теплового аэростата уменьшается. Чтобы оценить количественно это влияние, необходимо в формулу (6) подставить значение газовой постоянной для влажного воздуха. При 100% влажности и температуре окружающего воздуха 20 градусов подъемная сила уменьшается на 1% по сравнению с абсолютно сухим воздухом, а при 40 градусах это уменьшение составит уже 3%, что для аэростата класса АХ-7 даст уменьшение подъемной силы на 15...20 кг.
Хотя влияние влажности и невелико, но в некоторых случаях, например при проведении полетов в тропических условиях, пилоту это влияние необходимо учитывать.