Аэронавигационные карты

Карта является основным инструментом для ориентирования. Наиболее удобными для использования при полетах на тепловых аэростатах являются карты масштаба 1:100 000 (1 см соответствует 1 км) и 1:50 000 (1 см соответствует 0,5 км). Карты 1:100 000 используются для прогулочных, рекламных и тренировочных полетов, при организации соревнований предпочтение отдается картам масштаба 1:50 000, по которым можно точно оценить результат спортсмена. Чтобы узнать, сколько километров содержится в одном сантиметре, необходимо во втором числе масштаба отбросить пять нулей.

Все карты условно делятся на общегеографические и специальные. К общегеографическим относятся топографические и гидрографические карты, первые подробно отображают земную поверхность, вторые - водные пространства и глубины. Специальные карты отличаются от общегеографических тематической направленностью, такими картами являются аэронавигационные, автодорожные, административные и другие.

Для нужд воздухоплавания специальных аэронавигационных карт не выпускается. Приходится приобретать топографические карты подходящего масштаба и с аэронавигационных карт, которые имеют масштаб 1:500 000 и более мелкий, переносить на них необходимую информацию.

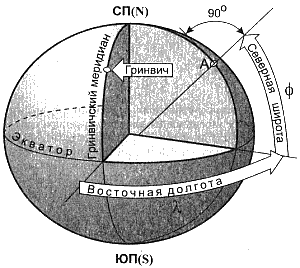Земля для построения карт представляется в виде эллипсоида (см. рис. 12.1) с длиной меридиана 40 008 548 м и длиной экватора 40 075 704 м. Средний радиус земли равен 6 371 110 м. Точки, в которых ось суточного вращения пересекается с поверхностью земного эллипсоида, называются географическими полюсами. Для определения места на земной поверхности пользуются системой географических координат или системой плоских прямоугольных координат. Рис. 12.1. Земной эллипсоид и определение географических координат точки А

В системе географических координат нахождение точки А определяется широтой φ и долготой λ. За ноль отсчета принимается точка пересечения экватора и Гринвичского меридиана (меридиана, проходящего через город Гринвич, находящийся в Англии). Широта изменяется от 0 до 90° в сторону Северного полюса (северная широта ) и от 0 до 90° в сторону Южного полюса (южная широта). Линии с точками одинаковой широты называются параллелями. Долгота изменяется от 0 до 180° в сторону запада от Гринвичского меридиана (западная долгота)и от 0 до 180° в сторону востока (восточная долгота). Система географических координат из-за небольшой протяженности полетов до недавнего времени в тепловом воздухоплавании практически не применялась. С появлением Глобальной навигационной системы GPS (Global Position System) с помощью устройства по размеру немногим более пачки сигарет стало возможным с точностью до нескольких метров определять географические координаты, скорость, направление движения и многие другие величины, связанные с навигационными задачами. Такие приборы особенно удобны при участии в соревнованиях и полетах в незнакомой местности.

На топографических картах масштабов 1:25 000... 1:200 000 географические координаты наносятся на шкалы, расположенные на рамках каждого листа (см. рис. 12.4), на картах масштаба 1:500 000 и более мелких линии параллелей и меридианов нанесены в виде сетки на поле самой карты.

Карта по своей сути является уменьшенной разверткой земного эллипсоида на плоскость. В зависимости от назначения карт применяются разные способы развертывания, сводящие к минимуму те или иные искажения. Для топографических карт масштабов 1:25 000... 1:500 000 используется единая равноугольная проекция Гаусса.

В системе плоских прямоугольных координат земная поверхность представляется в виде шестидесяти шести градусных секторов, которые с очень малыми искажениями могут быть развернуты на плоскость (проекция Гаусса). Эти сектора, ограниченные меридианами, называются долготными зонами (см. рис. 12.2).

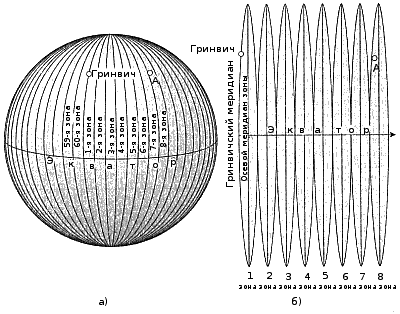За первую зону принимается зона, левый меридиан которой проходит через Гринвич. Россия начинается с 4-й и заканчивается в 33-й долготной зоне. Искажения в этом методе развертывания отсутствуют вдоль осевого меридиана каждой зоны, возрастают вблизи краевых меридианов и составляют не более 0,1 % от измеряемых длин. Для навигационных воздухоплавательных задач такими искажениями можно пренебречь и при проведении измерений не учитывать.

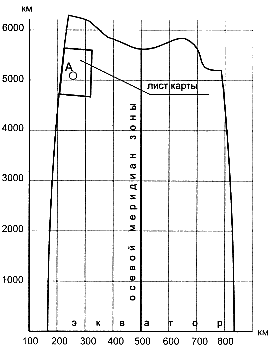Каждая долготная зона (см. рис. 12.3) имеет свою прямоугольную систему координат, за ось абсцисс принимается линия экватора, а за ось ординат — линия, проходящая на 500 км левее осевого меридиана зоны. Листы карт земной поверхности, представляющие равносторонние трапеции, укладываются на развертку зоны соответствующего масштаба так, чтобы боковые стороны были параллельны меридианам, поэтому при склейке всех листов зоны можно получить плоскую масштабную развертку земной поверхности. Рис. 12.3. Координатная километровая сетка, наложенная на долготную шестиградусную зону На картах масштабов 1:25 000 ... 1:200 000, как правило, наносится прямоугольная координатная сетка с шагом в один километр, поэтому такая сетка называется также километровой.

На рисунке 12.4 в качестве примера показан кусок карты масштаба 1:50 000. На ней нанесена прямоугольная координатная сетка и на полях градусная шкала географических координат, каждый черный или белый элемент которой имеет размер в 1'. В нижней части приводится схема магнитного склонения и отклонения вертикальных линий сетки от истинного направления на север (сближение меридианов), также комментарий к этой схеме, который не дает никаких шансов перепутать направления поправок.

Магнитным склонением называется угол между истинным направлением на север (истинным меридианом) и показаниями магнитной стрелки компаса (магнитным меридианом).

Сближением меридианов называется угол между истинным меридианом и вертикальной километровой линией, который зависит от удаления от осевого меридиана зоны и может иметь значение от 0 до ±3°. На карте показывается средний угол для данного листа.
Чтобы узнать координаты точки А (перекресток на рис. 12.4) в системе географических координат, необходимо из этой точки провести перпендикуляры на ближайшие рамки карты, указанная точка имеет координаты:

45°03'58" СШ
42°02'25" ВД.

Координаты той же точки, но записанные в системе плоских прямоугольных координат, имеют значения:

5 047 800 м;
(8) 266 700 м.

Таким образом, точка А удалена от экватора на 5 047 800 м и находится на расстоянии 266 700 м от начала координат 8-й зоны.

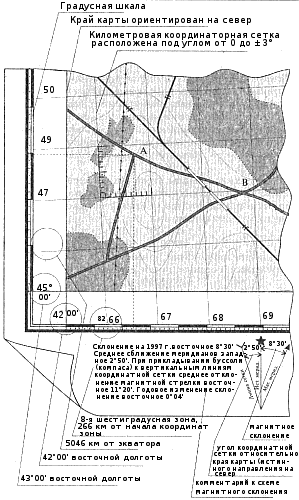При проведении соревнований на тепловых аэростатах координаты целей определяются с использованием километровой сетки, но в отличие от общепринятой системы координаты определяются не в метрах, а в номерах квадратов. Каждая точка идентифицируется 8-значным числом: первые две цифры соответствуют номеру квадрата по восточному направлению, вторые две являются сотыми долями этого квадрата, затем указывается номер квадрата по северному направлению и соответственно сотые этого квадрата. Если вы еще не забыли, какой порядок указания координат в математике, то в спортивном воздухоплавании он точно такой же, сначала указывается значение по оси X, затем по Y. Например, тот же перекресток А на рис. 12.4 будет иметь координаты: 6670/4780. Рис. 12.4. Внешний вид топографической карты масштаба 1:50000 Обратите внимание, что в отличие от географической и координатной системы в спортивном воздухоплавании сначала указывается координата восток-запад, а затем юг-север.

Пилоту аэростата необходимо знать условные обозначения, которые применяются в топографических и навигационных картах, многие из них, конечно, знакомы вам еще из школы. Полный перечень можно посмотреть в специальной литературе.

Основные условные обозначения линейных и высотных ориентиров приведены на рисунке 12.5. Хорошо запомните обозначения линий электропередач и электрифицированных железных дорог, самое большое количество аварий аэростатов с печальным исходом происходит именно при столкновении с этими препятствиями. При подготовке карты имеет смысл дополнительно выделять ЛЭП.

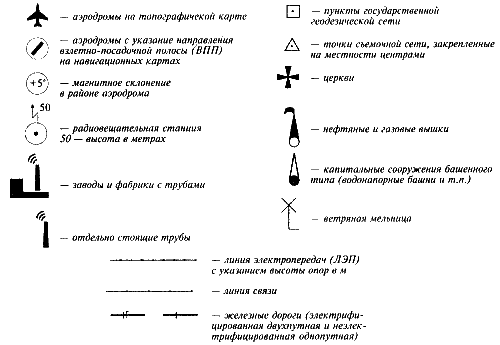
Рис. 12.5. Некоторые условные обозначения на картах

Источник: Таланов А. В. Все о воздушных шарах.
Москва, Издательство Астрель, 2002.